Fast Nonlinear Least Squares Optimization of Large-scale Semi-sparse Problems
Abstract
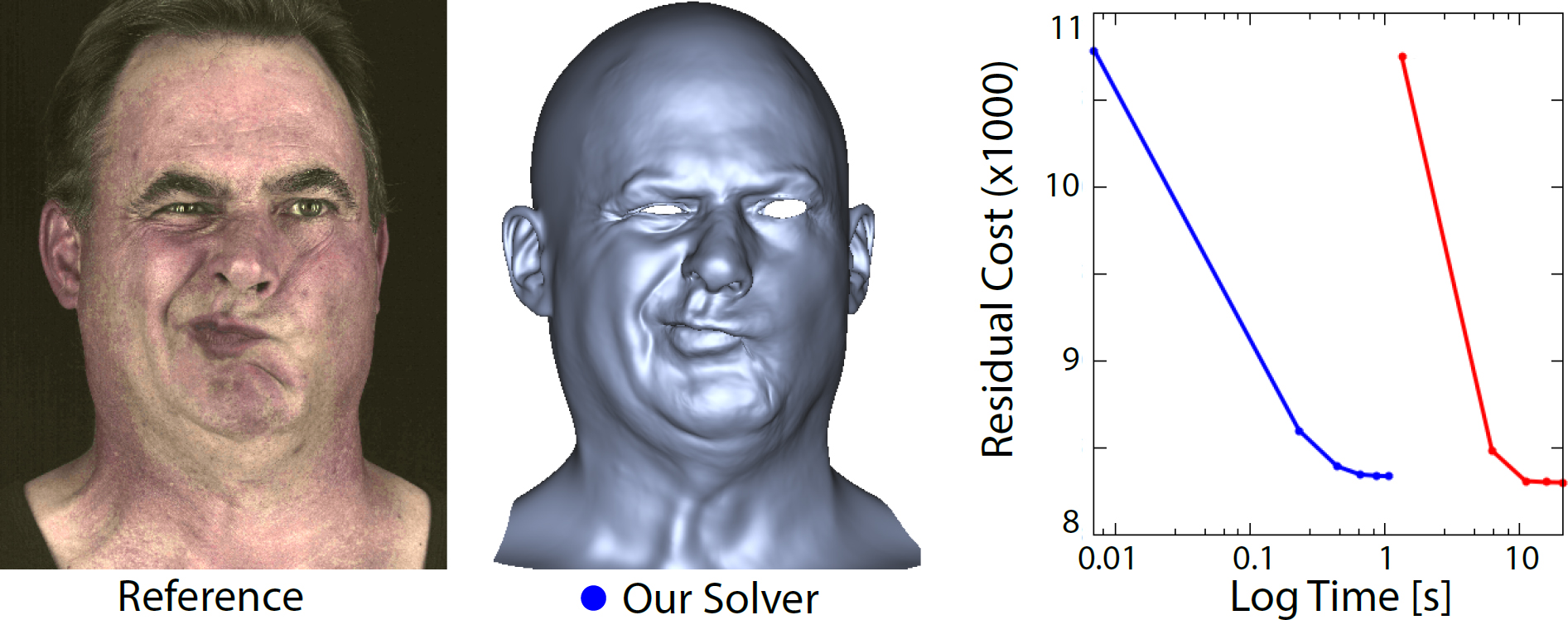
Many problems in computer graphics and vision can be formulated as a nonlinear least squares optimization problem, for which numerous off-the-shelf solvers are readily available. Depending on the structure of the problem, however, existing solvers may be more or less suitable, and in some cases the solution comes at the cost of lengthy convergence times. One such case is semi-sparse optimization problems, emerging for example in localized facial performance reconstruction, where the nonlinear least squares problem can be composed of hundreds of thousands of cost functions, each one involving many of the optimization parameters. While such problems can be solved with existing solvers, the computation time can severely hinder the applicability of these methods. We introduce a novel iterative solver for nonlinear least squares optimization of large-scale semi-sparse problems. We use the nonlinear Levenberg-Marquardt method to locally linearize the problem in parallel, based on its first- order approximation. Then, we decompose the linear problem in small blocks, using the local Schur complement, leading to a more compact linear system without loss of information. The resulting system is dense but its size is small enough to be solved using a parallel direct method in a short amount of time. The main benefit we get by using such an approach is that the overall optimization process is entirely parallel and scalable, making it suitable to be mapped onto graphics hardware (GPU). By using our minimizer, results are obtained up to one order of magnitude faster than other existing solvers, without sacrificing the generality and the accuracy of the model. We provide a detailed analysis of our approach and validate our results with the application of performance-based facial capture using a recently-proposed anatomical local face deformation model.